As shown above, December 8 is the 150th anniversary of James Clerk Maxwell’s presentation on electromagnetic theory to the Royal Society in London. While the 4 equation for the interaction of electric and magnetic fields that we techies know well were not written in the current form for another 20 years, the basic theory was all there in complex form involving 20 equations. (Oliver Heaviside, who is mentioned parenthetically in a song in the musical Cats, was later responsible for the 4 equation version and the modern vector notation.)

Maxwell showed how previous electrical and magnetic observations were all consistent and related to each other and also predicted electromagnetic waves, e.g. radio and light. Maxwell died in 1879. In 1886 Heinrich Hertz of Technische Hochschule (now the Karlsruhe Institute of Technology) in Karlsruhe, Germany demonstrated that electromagnetic waves/radio waves actually exist.

The current issue of IEEE Spectrum magazine has a nice article for general audiences on how this all came about and its significance. Below are the 4 equations, in differential form - physicists often prefer the integral form - along with Spectrum’s brief summary.

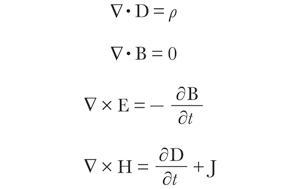
Today, the relationship between electricity and magnetism, along with the wave nature of light and electromagnetic radiation in general, is encoded in the four “Maxwell’s equations” shown above. The equations can be written in different ways. Here, J is the current density. E and B are the electric and magnetic fields, respectively. And there are two other fields, the displacement field D and the magnetic field H. These fields are related to E and B by constants that reflect the nature of the medium that the fields pass through (the values of these constants in vacuum can be combined to give the speed of light). The displacement field D was one of Maxwell’s key contributions, and the last equation describes how both current and changing electric fields can give rise to magnetic fields. The symbols at the beginning of each equation are differential operators. These compactly encode calculus that involves vectors, quantities that have a directionality and thus x, y, and z components. Maxwell’s original formulation of his electromagnetic theory contained 20 equation

Tags: History